点群・ポリゴン処理 地形データ活用 ドローン
航空測量からの地形データ活用方法 4 ~鉄塔配置、電線(カテナリー曲線)定義と近傍樹木データの抽出~
航空測量からの地形データ活用方法3では、航空測量データから地形データと樹木データの分離、さらに曲率から人工物の抽出までを紹介させていただきました。
今回は、地形データに対して鉄塔を配置した場合の「切り土の計算」と、「電線定義」の2つの研究成果をご紹介いたします。
今回の研究に使用される技術は、ポリゴンのブーリアン演算とカテナリー曲線の定義とNURBS近似変換処理になります。
切り土計算
切り土の計算は以下の処理になります。
- 鉄塔の3DモデルをCADデータとして用意
- 鉄塔を配置する位置を山肌地形ポリゴンに対して任意に指示
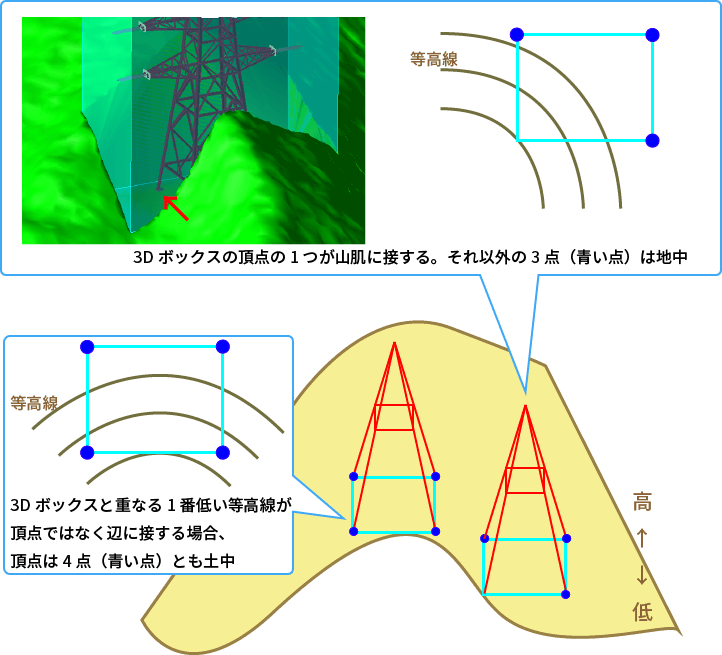
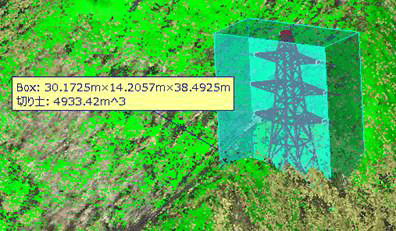
- 鉄塔モデルを包含する3Dボックスを内部で定義
- 3Dボックスを山肌地形に潜らせる処理を行う
- 3Dボックスを土中に潜らせる深さは、3頂点が土中、1頂点のみ山肌に接する状態とする
- 5の処理で決めた高さでボックスに包含される体積を計算する
この体積が切り土量となる

電線定義
電線定義の処理は以下の処理となります。
ロープや電線などを両端固定で垂らした曲線は、カテナリー曲線(懸垂曲線)となります。
有名な建造物としては、世界遺産サクラダファミリアがあります。建築家ガウディは、このカテナリー曲線を用いて、サクラダファミリアの輪郭を定義したそうです。

3D CADの内部にはカテナリー曲線を保持する構造を持っていないため、3D CADで持てる曲線式のNURBSに近似変換して電線を定義します。
以下にカテナリー曲線の式を導出します。
両端が固定された電線を含む平面内で、水平方向に $x$ 軸、鉛直上方に $y$ 軸をとり、電線の線密度(単位長さの質量)を$\sigma_0$(一定)、電線のある点から電線に沿って測った長さを $s$、電線の張力を $T$ とします。
電線の微小部分に働く水平方向の張力の釣り合いを考えると
\[ dT_x=0 \]
鉛直方向の釣り合いは、微小部分の重さが $\sigma_0g\,ds$ であることから
\[ dT_y= \sigma_0g\,ds \]
したがって
\[ \frac{dT_x}{ds}=0, \quad \frac{dT_y}{ds}= \sigma_0g \]
となります。
この2式を積分すると、$T_x=T\frac{dx}{ds}$, $T_y=T\frac{dy}{ds}$であることから
\[ T_x=T\frac{dx}{ds}=T_0(一定), \quad T_y=T\frac{dy}{ds}= \sigma_0gs \]
となります。ただし電線の最下点を $s=0$ としました。この2式の比をとれば
\[ \frac{dy}{dx}=\frac{ \sigma_0 g}{T_0}s \]
$ds= \sqrt {1+ \left (\frac{dy}{dx}\right)^2} dx$ であることから、微分して
\[ \frac{d^2 y}{dx^2}=\frac{\sigma_0 g}{T_0} \sqrt {1+ \left ( \frac{dy}{dx} \right) ^2} \]
となります。
この微分方程式の解は $a=\frac{T_0}{ \sigma_0 g}$, $C_1$, $C_2$ を定数として
\[ y=a \cosh \left(\frac{x}{a}+C_1 \right)+C_2 \]
となります。これがカテナリー曲線の式となります。
(参考文献: 戸田盛和, 一般力学30講, 朝倉書店, 1994.)
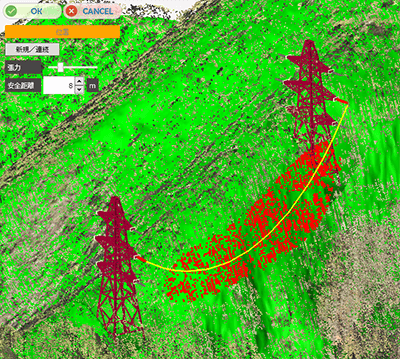
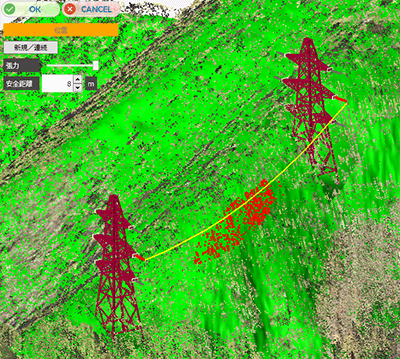
電線の作成は以下の処理になります。
- 電線の両端を指示する
- 張力パラメータを指定する
- 指定されたパラメータでカテナリー曲線を定義する
- カテナリー曲線をNURBSに近似変換し、表示する
- 定義された電線に近い樹木データを検知し、警告表示する
研究担当

ACE事業部 堀 玄洋
2014年、(株)アルモニコス入社。
主に受託開発やパッケージソフトClassNK-PEERLESS、spGateの開発を担当。
趣味は語学(韓国語、英語)、ピアノ。好きな作曲家はショパンとスクリャービン。

A-Pro事業部 金秉訓(キムビョンフン)
2012年、(株)アルモニコスに入社。
入社後から韓国へのパッケージソフトの営業や技術サポートを実施。2018年からは国内にて、主にClassNK-PEERLESSの営業を行っている。
趣味は、映画、グルメ旅(ラーメン、辛い物)、ビリヤード。


※所属・肩書は記事掲載時のものであり、現在とは異なる場合があります。
